[课程资料] 高级统计方法书后习题（三）

本系列内容为《统计学习导论——基于R应用》（机械工业出版社）部分课后习题答案。

本章为3.7节习题答案。

声明：本博客中的习题分享仅供学习和参考之用。请勿将其用于任何形式的学术欺骗、抄袭或违反学术诚信的行为。尊重知识，诚实学习。

如果您发现文章内容中任何不妥或错误之处，请随时通过联系方式或评论功能与我交流，以便我进行改正和完善。

一、概念题

3.7.2

• KNN算法：即K近邻算法，通过判断某个样本与训练集中样本的距离来进行预测（通过找出最类似的“邻居”来进行预测）。KNN的核心思想是在要对一个新样本进行预测时，先计算距离，找出预测点的最近K个近邻点，并根据这些近邻的特征来进行预测。

• KNN分类：根据最近的K个近邻点的类别占比，找出出现最多的类别，并对预测点进行预测。预测结果是定性的（例如，对垃圾邮件和普通邮件进行分类）。

• KNN回归：根据最近的K个近邻点的平均值来对预测点进行预测。预测结果是定量的值（例如，估计房价）。

3.7.5

二、应用题

3.7.9

• (a)

  # 9.(a)
  library(ISLR) # 导入ISLR包
  Auto # 查看Auto数据集
  pairs(Auto) # 使用Auto中的所有变量绘制散点图矩阵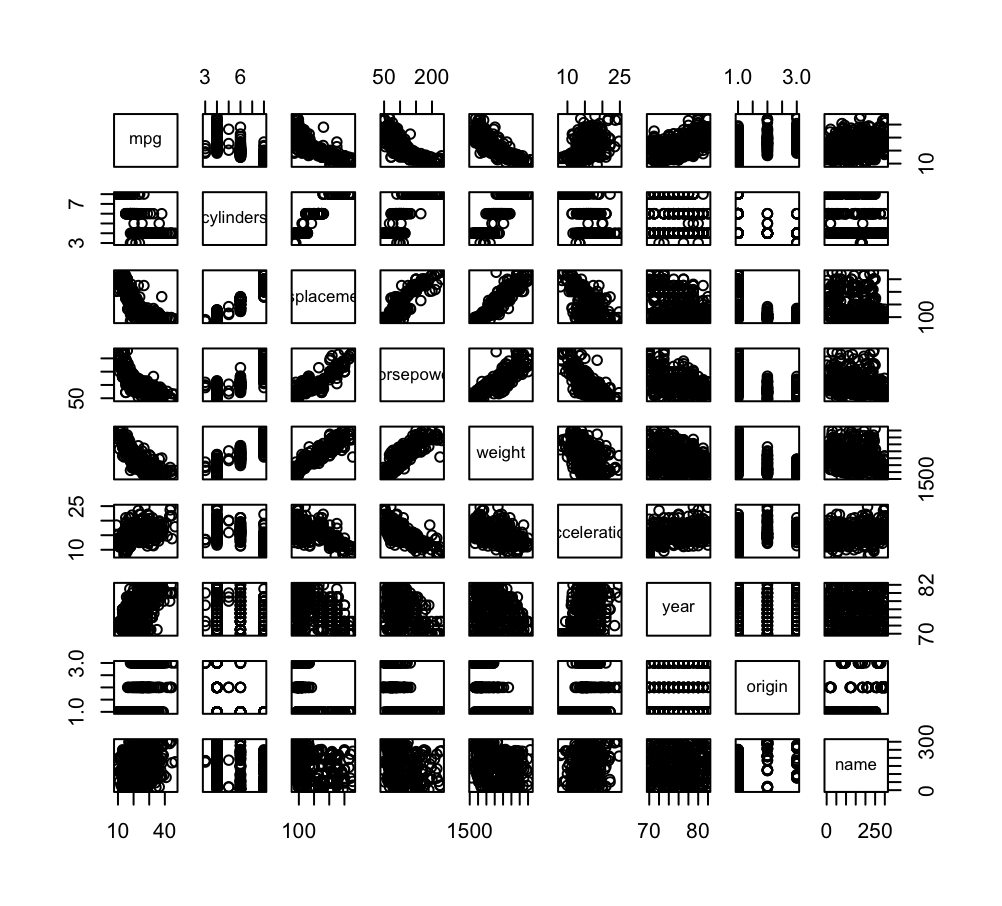

  

• (b)

  # 9.(b)
  cor(subset(Auto, select= -name)) # 计算Auto数据集中所有数值变量的相关性矩阵（除去定性变量name）
  ## 相关系数矩阵中 1表示完全正相关 -1表示完全负相关 0表示变量没有线性关系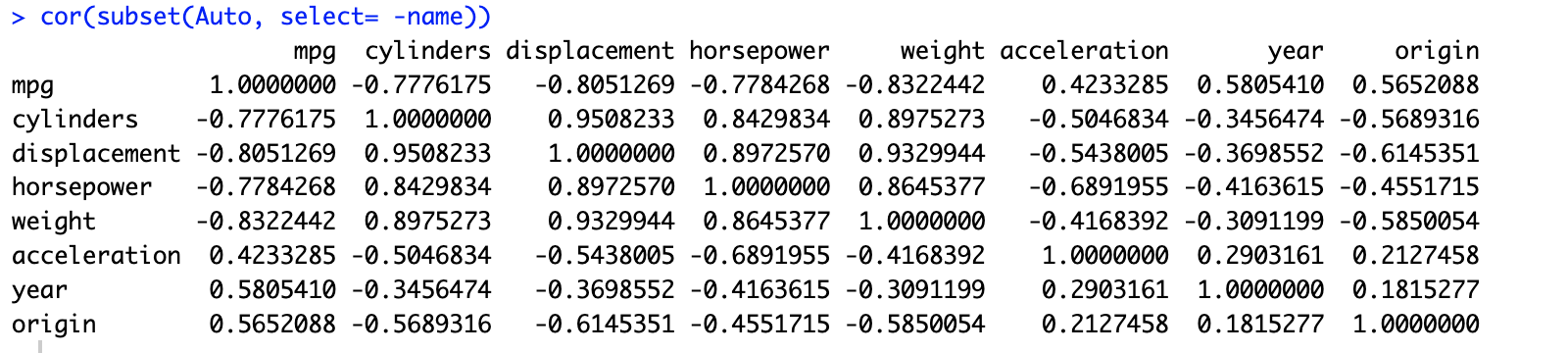

  

• (c)

  # 9.(c)
  model = lm(mpg ~ (.-name), data = Auto) # 使用除了name之外的所有变量作为预测变量，mpg作为响应变量进行线性拟合
  summary(model)
  ## i.通过线性拟合模型的F统计量为252.4和p值为<2.2e-16（远小于0.05）说明拒绝零假设（预测变量与响应变量无关），则说明预测变量和响应变量有关。
  ## ii.从各个预测变量的p值来看，displacement、weight、year和origin几个变量与mpg之间有显著的线性关系。
  ## iii.年龄的系数约为0.75，说明mpg与年龄正线性相关，并且年龄平均增加1个单位，mpg增加约0.75个单位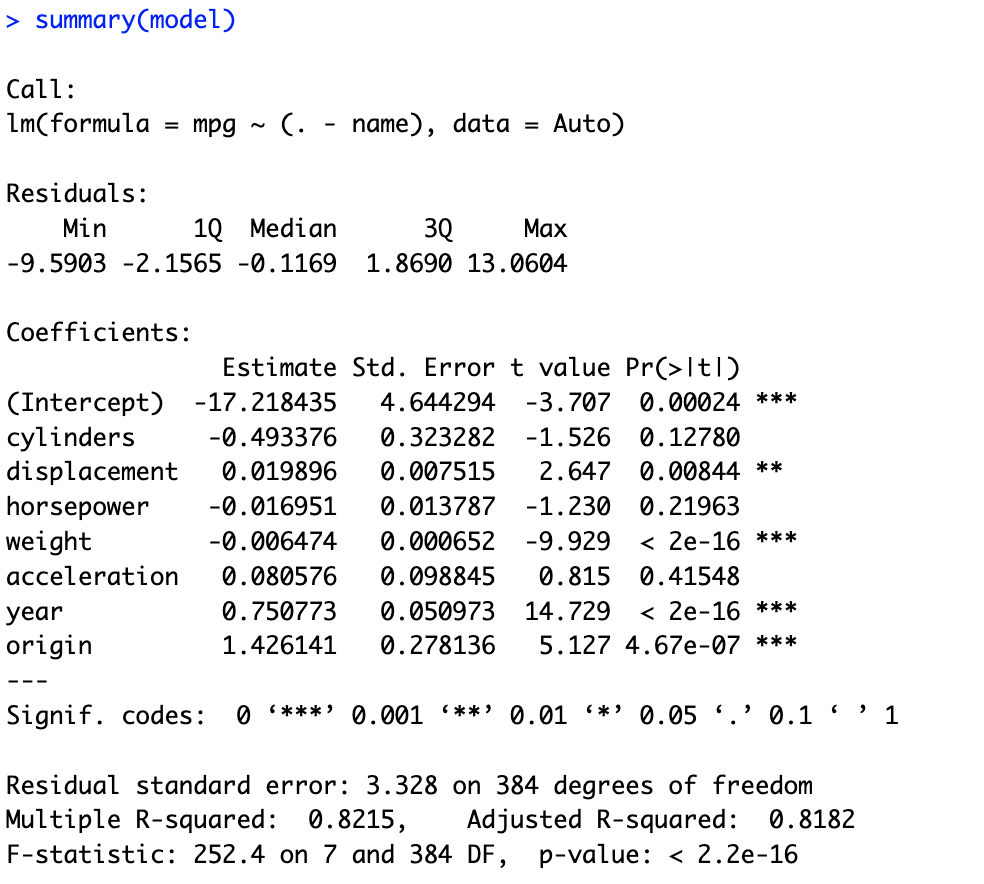

  

• (d)

  # 9.(d)
  par(mfrow=c(2,2))
  plot(model) # 绘制model拟合模型的诊断图
  ## 根据残差图可以看出整体均匀分布在0附近，但是也能看出承先下降再上升趋势，可能存在变量与mpg之间是非线性关系
  ## QQ图可以看出误差项基本符合正态分布
  ## S-L图中标准化残差平方根随机分布，说明没有异方差性
  ## 图中可以发现有明显的离群点、高杠杆点，表明可能存在异常值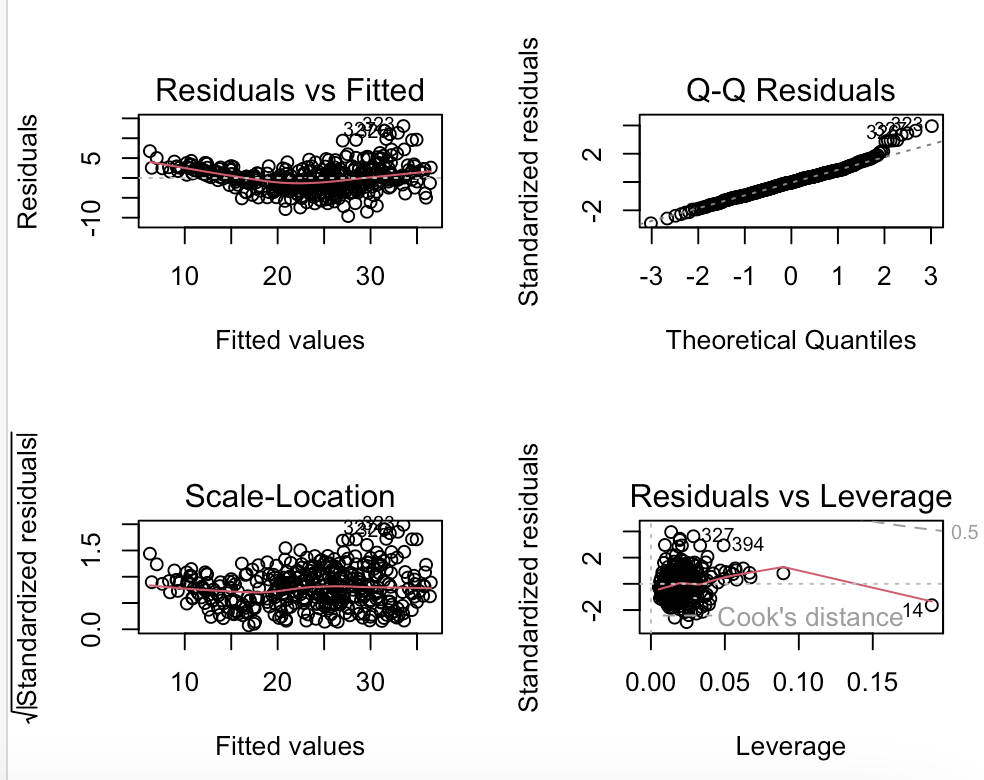

  

• (e)

  # 9.(e)
  model_interactive = lm(mpg ~ displacement*weight+horsepower:weight+year*horsepower, data = Auto) 
  summary(model_interactive)
  ## 根据结果发现，displacement与weight、horsepower与year之间都有比较强的交互作用（p值小于0.05）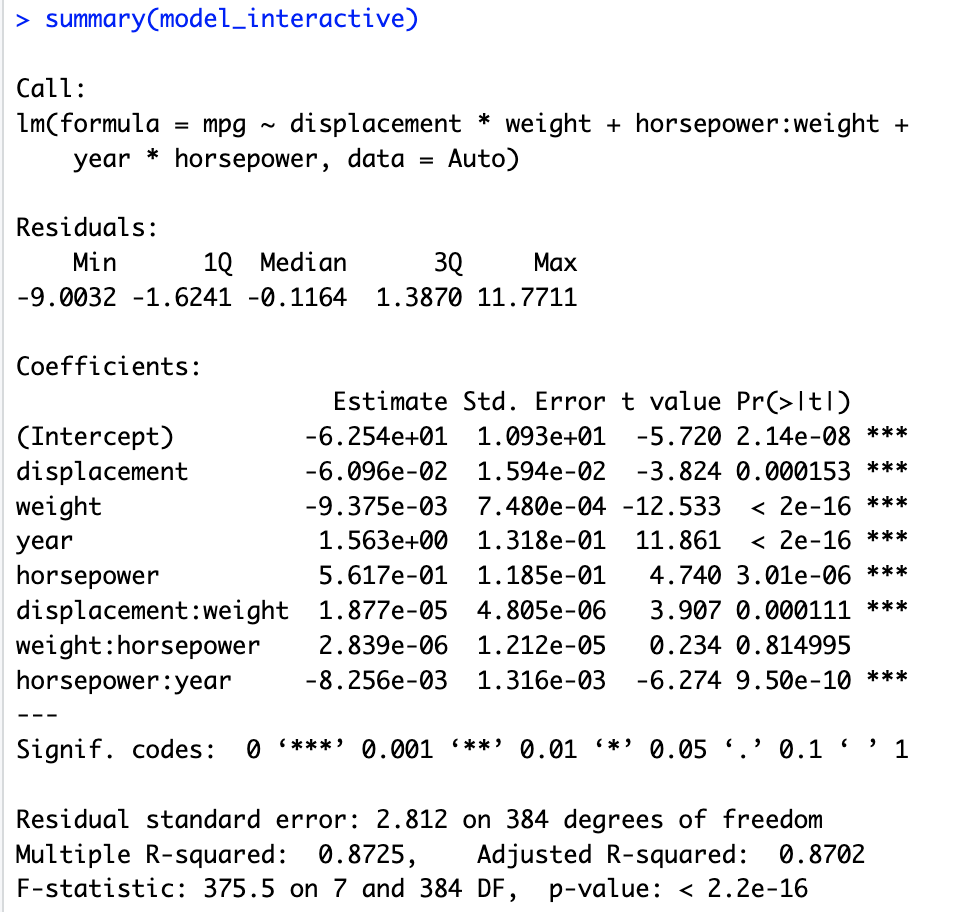

  

• (f)

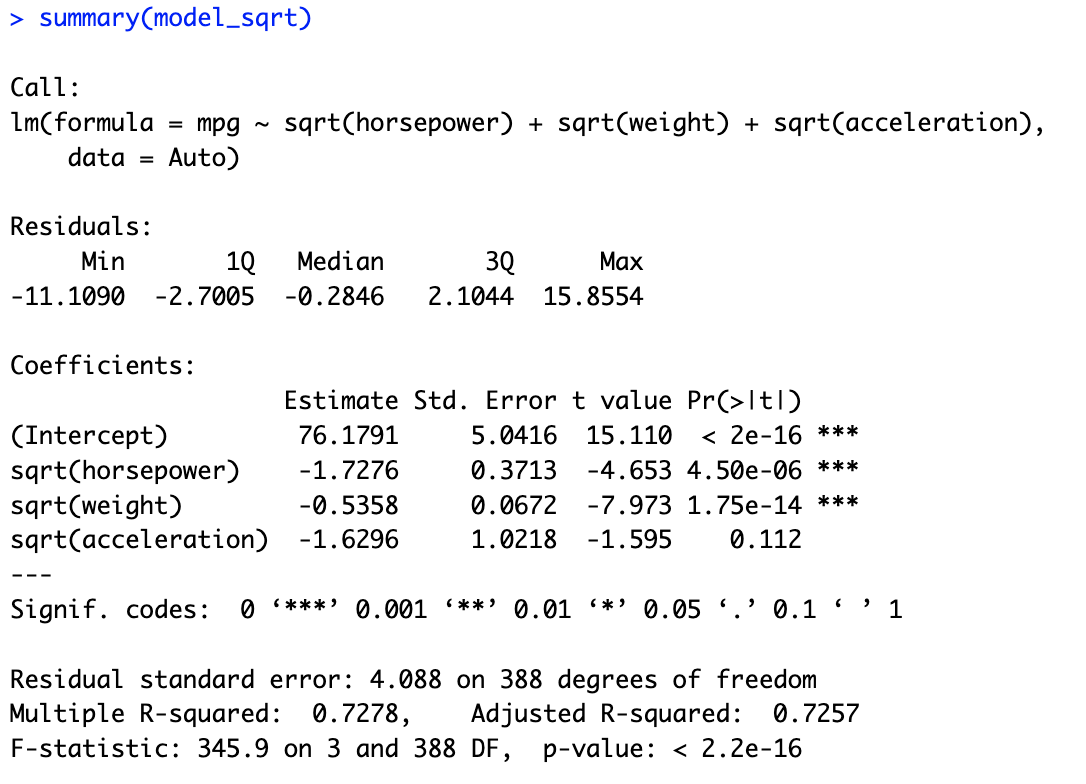
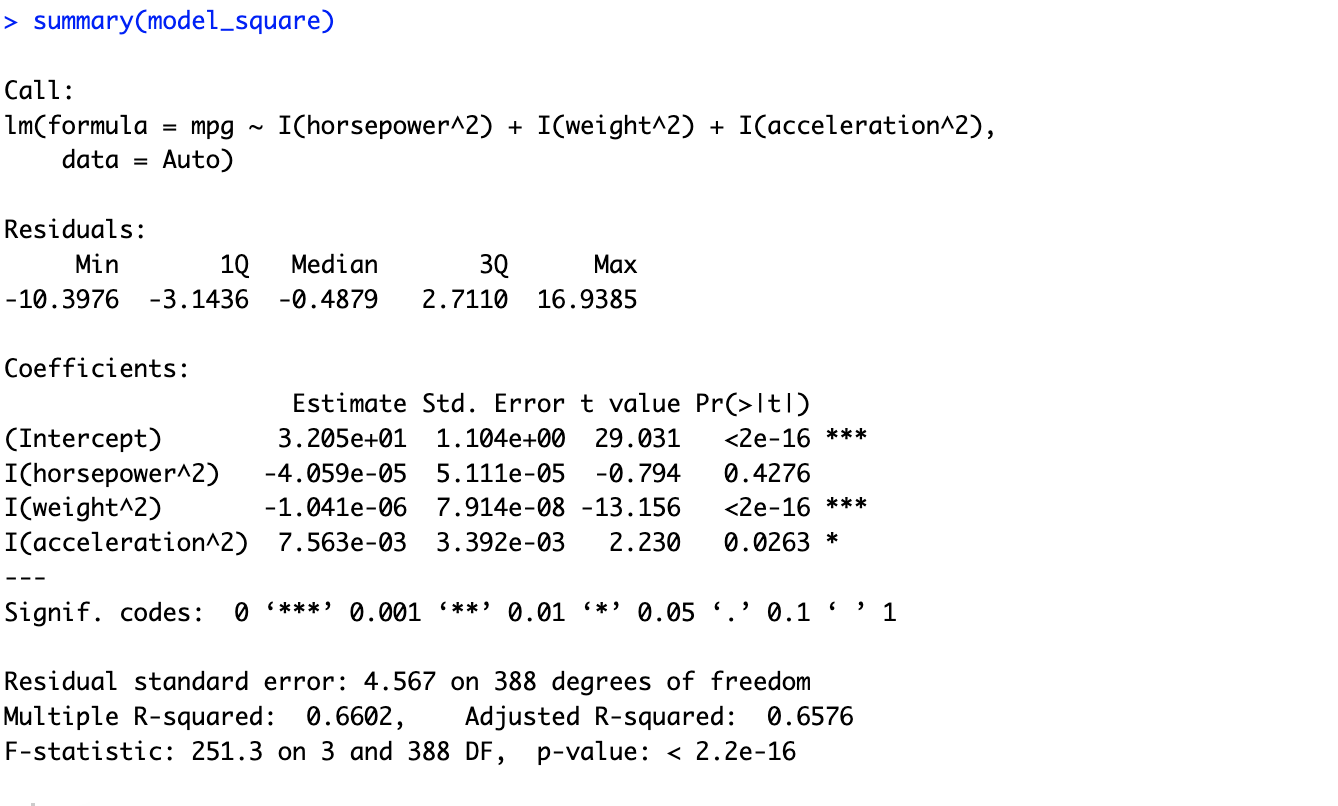
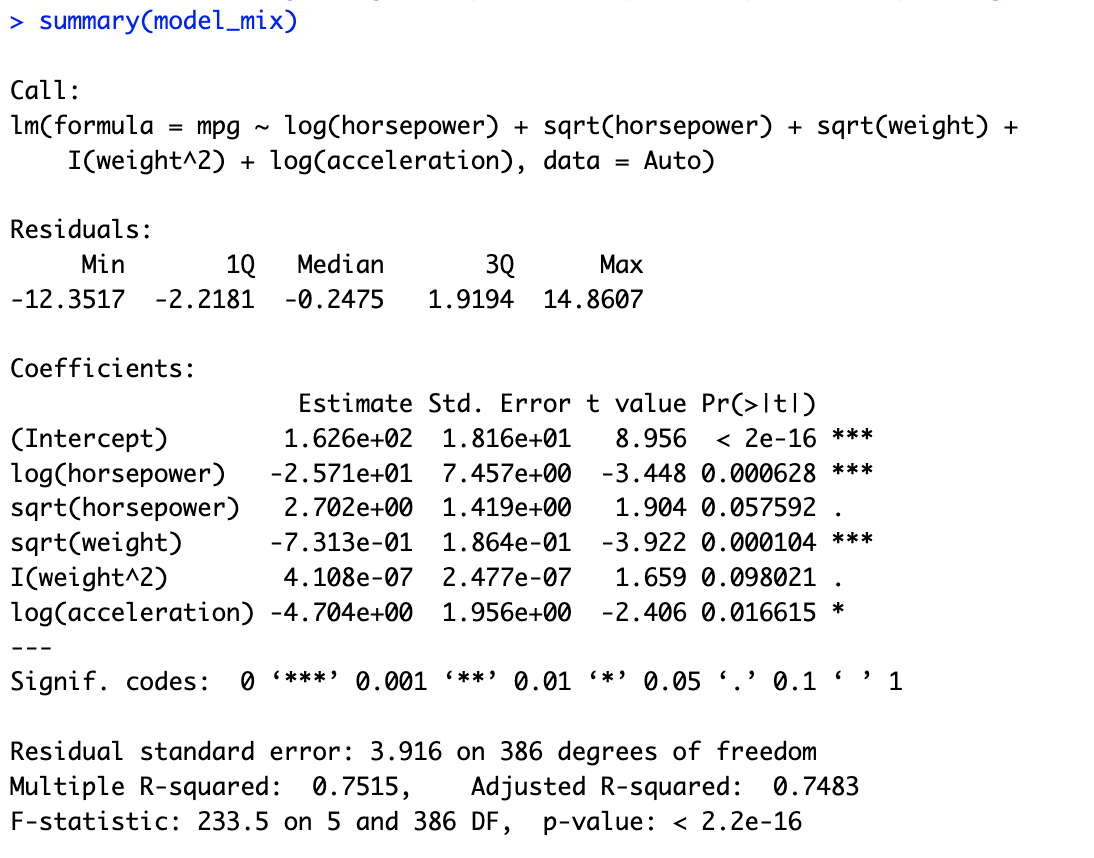
  # 9.(f) 
  ## 选择horsepower weight acceleration作为预测变量
  model_log = lm(mpg ~ log(horsepower) + log(weight) + log(acceleration), data = Auto)
  summary(model_log)
  model_sqrt = lm(mpg ~ sqrt(horsepower) + sqrt(weight) + sqrt(acceleration), data = Auto)
  summary(model_sqrt)
  model_square = lm(mpg ~ I(horsepower^2) + I(weight^2) + I(acceleration^2), data = Auto)
  summary(model_square)
  model_mix = lm(mpg ~ log(horsepower) + sqrt(horsepower) + sqrt(weight) + I(weight^2) + log(acceleration), data = Auto)
  summary(model_mix)
  ## 在多次尝试后，发现用model_mix的拟合方法进行拟合R方比较大，说明拟合效果比较好。

  

  

  

  

• 完整代码

  # 9.(a)
  library(ISLR) # 导入ISLR包
  Auto # 查看Auto数据集
  pairs(Auto) # 使用Auto中的所有变量绘制散点图矩阵
  ​
  # 9.(b)
  cor(subset(Auto, select= -name)) # 计算Auto数据集中所有数值变量的相关性矩阵（除去定性变量name）
  ## 相关系数矩阵中 1表示完全正相关 -1表示完全负相关 0表示变量没有线性关系
  ​
  # 9.(c)
  model = lm(mpg ~ (.-name), data = Auto) # 使用除了name之外的所有变量作为预测变量，mpg作为响应变量进行线性拟合
  summary(model)
  ## i.通过线性拟合模型的F统计量为252.4和p值为<2.2e-16（远小于0.05）说明拒绝零假设（预测变量与响应变量无关），则说明预测变量和响应变量有关。
  ## ii.从各个预测变量的p值来看，displacement、weight、year和origin几个变量与mpg之间有显著的线性关系。
  ## iii.年龄的系数约为0.75，说明mpg与年龄正线性相关，并且年龄平均增加1个单位，mpg增加约0.75个单位
  ​
  # 9.(d)
  par(mfrow=c(2,2))
  plot(model) # 绘制model拟合模型的诊断图
  ## 根据残差图可以看出整体均匀分布在0附近，但是也能看出承先下降再上升趋势，可能存在变量与mpg之间是非线性关系
  ## QQ图可以看出误差项基本符合正态分布
  ## S-L图中标准化残差平方根随机分布，说明没有异方差性
  ## 图中可以发现有明显的离群点、高杠杆点，表明可能存在异常值
  ​
  # 9.(e)
  model_interactive = lm(mpg ~ displacement*weight+horsepower:weight+year*horsepower, data = Auto) 
  summary(model_interactive)
  ## 根据结果发现，displacement与weight、horsepower与year之间都有比较强的交互作用（p值小于0.05）
  ​
  # 9.(f) 
  ## 选择horsepower weight acceleration作为预测变量
  model_log = lm(mpg ~ log(horsepower) + log(weight) + log(acceleration), data = Auto)
  summary(model_log)
  model_sqrt = lm(mpg ~ sqrt(horsepower) + sqrt(weight) + sqrt(acceleration), data = Auto)
  summary(model_sqrt)
  model_square = lm(mpg ~ I(horsepower^2) + I(weight^2) + I(acceleration^2), data = Auto)
  summary(model_square)
  model_mix = lm(mpg ~ log(horsepower) + sqrt(horsepower) + sqrt(weight) + I(weight^2) + log(acceleration), data = Auto)
  summary(model_mix)
  ## 在多次尝试后，发现用model_mix的拟合方法进行拟合R方比较大，说明拟合效果比较好。

3.7.10

• (a)

  # 10.(a)
  library(ISLR)
  Carseats # 展示Carseats数据集
  model = lm(Sales ~ Price+Urban+US, data = Carseats) # 使用Price+Urban+US对Sales进行多远线性拟合
  summary(model)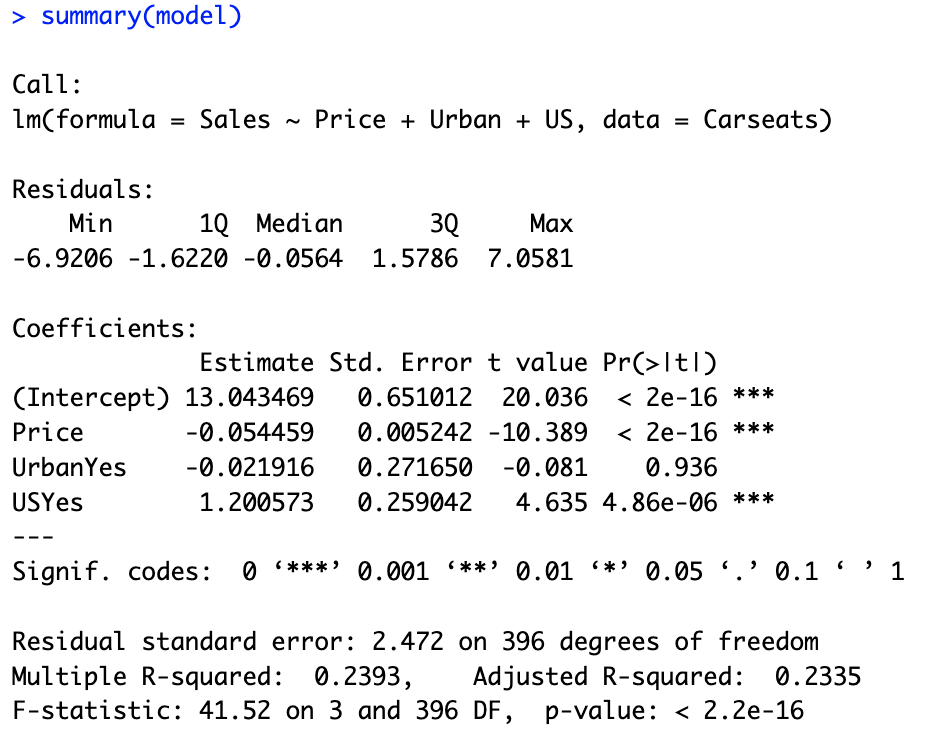

  

• (b)

  # 10.(b)
  ## Price（p值<0.05）:系数约为-0.05，说明Price每增加一个单位，Sales会随之减少0.05个单位，两者成负相关。
  ## Urban（p值>0.05）:系数约为-0.02，Urban是一个二分类的哑变量，说明Urban为Yes相对于为No的情况下，Sales会减少0.02个单位。
  ## 但是Urban变量对应P值>0.05，说明该变量对Sales并没有显著影响。
  ## US（p值<0.05）:系数约为1.2，US也是一个二分类哑变量，说明US为Yes相对于为No，Sales会增加1.2个单位。

• (c)

  # 10.(c)
  ## Sales = 13.04 - 0.05*Price - 0.02*(Urban=Yes) + 1.2*(US = Yes)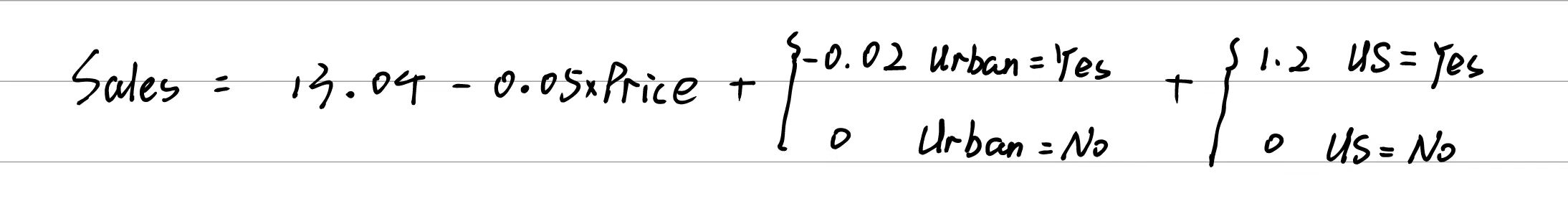

  

• (d)

  # 10.(d)
  ## 根据(a)中得到的p值，Price、US可以拒绝零假设，Urban不能拒绝零假设。

• (e)

  # 10.(e)
  model_min = lm(Sales ~ Price+US, data = Carseats) # 仅使用Price和US对Sales进行拟合
  summary(model_min)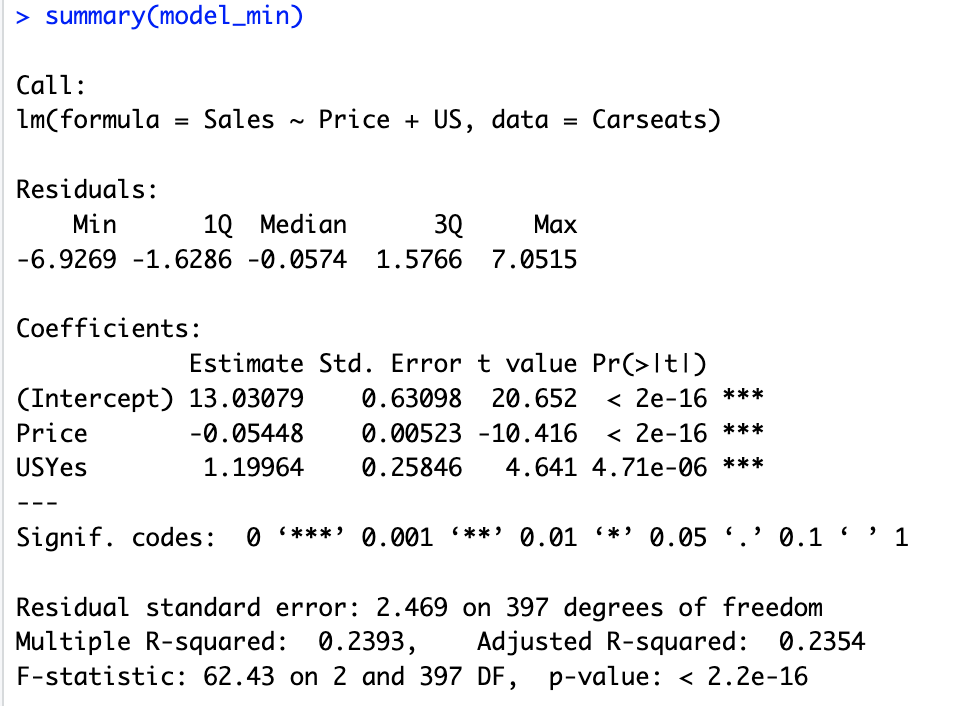

  

• (f)

  # 10.(f)
  ## 从model的RSE为2.472 MR^2为0.2393 AR^2为0.2335
  ## 从model_min的RSE为2.469 MR^2为0.2393 AR^2为0.2354
  ## 两个模型都对数据进行了拟合，两者R^2相同，但是model_min的RSE和调整后R^2都比model表现的更好，拟合效果相对更好
  ## model_min的F统计量为62.42，而model为41.52，说明model_min在整体上更强

• (g)

  # 10.(g)
  confint(model_min)
  ## Price的置信区间为[-0.065, 0.044]
  ## USYes的置信区间为[0.692, 1.708]

  

• (h)

  # 10.(h)
  par(mfrow=c(2,2))
  plot(model_min) # 绘制诊断图
  ## 根据杠杆-残差图可以看出图中存在高杠杆点(杠杆值约0.05)和离群点（残差远离0）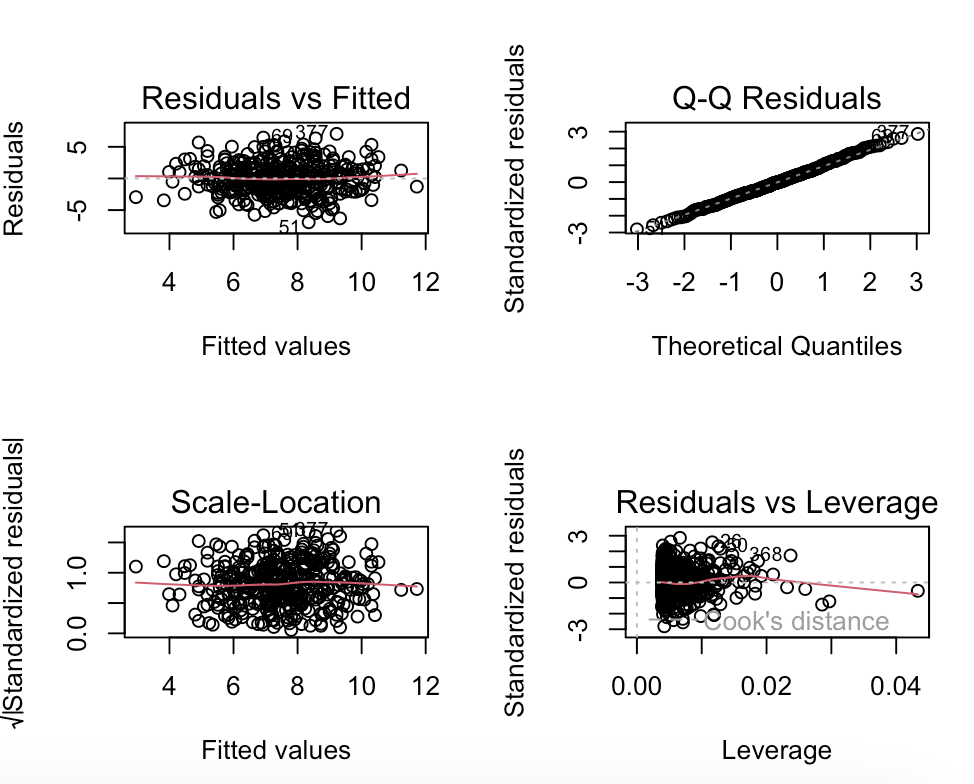

  

• 完整代码

  # 10.(a)
  library(ISLR)
  Carseats # 展示Carseats数据集
  model = lm(Sales ~ Price+Urban+US, data = Carseats) # 使用Price+Urban+US对Sales进行多远线性拟合
  summary(model)
  ​
  # 10.(b)
  ## Price（p值<0.05）:系数约为-0.05，说明Price每增加一个单位，Sales会随之减少0.05个单位，两者成负相关。
  ## Urban（p值>0.05）:系数约为-0.02，Urban是一个二分类的哑变量，说明Urban为Yes相对于为No的情况下，Sales会减少0.02个单位。
  ## 但是Urban变量对应P值>0.05，说明该变量对Sales并没有显著影响。
  ## US（p值<0.05）:系数约为1.2，US也是一个二分类哑变量，说明US为Yes相对于为No，Sales会增加1.2个单位。
  ​
  # 10.(c)
  ## Sales = 13.04 - 0.05*Price - 0.02*(Urban=Yes) + 1.2*(US = Yes)
  ​
  # 10.(d)
  ## 根据(a)中得到的p值，Price、US可以拒绝零假设，Urban不能拒绝零假设。
  ​
  # 10.(e)
  model_min = lm(Sales ~ Price+US, data = Carseats) # 仅使用Price和US对Sales进行拟合
  summary(model_min)
  ​
  # 10.(f)
  ## 从model的RSE为2.472 MR^2为0.2393 AR^2为0.2335
  ## 从model_min的RSE为2.469 MR^2为0.2393 AR^2为0.2354
  ## 两个模型都对数据进行了拟合，两者R^2相同，但是model_min的RSE和调整后R^2都比model表现的更好，拟合效果相对更好
  ## model_min的F统计量为62.42，而model为41.52，说明model_min在整体上更强
  ​
  # 10.(g)
  confint(model_min)
  ## Price的置信区间为[-0.065, 0.044]
  ## USYes的置信区间为[0.692, 1.708]
  ​
  # 10.(h)
  par(mfrow=c(2,2))
  plot(model_min) # 绘制诊断图
  ## 根据杠杆-残差图可以看出图中存在高杠杆点(杠杆值约0.05)和离群点（残差远离0）

3.7.14

• (a)

  # 14.(a)
  set.seed(1)  # 设置随机种子
  x1 = runif(100)  # 生成100个在[0, 1]均匀分布的随机数作为变量x1
  x2 = 0.5 * x1 + rnorm(100) / 10  # 生成变量x2，它与x1高度相关且带有一些随机噪声
  y = 2 + 2 * x1 + 0.3 * x2 + rnorm(100)  # 生成响应变量y，符合给定的线性模型，并添加一些随机噪声
  #回归系数 β0=2 β1=2 β2=0.3

  

• (b)

  # 14.(b)
  par(mfrow=c(1,1))
  cor(x1, x2)  # x1与x2之间的相关系数 0.8351
  plot(x1, x2)  # 绘制x1与x2之间散点图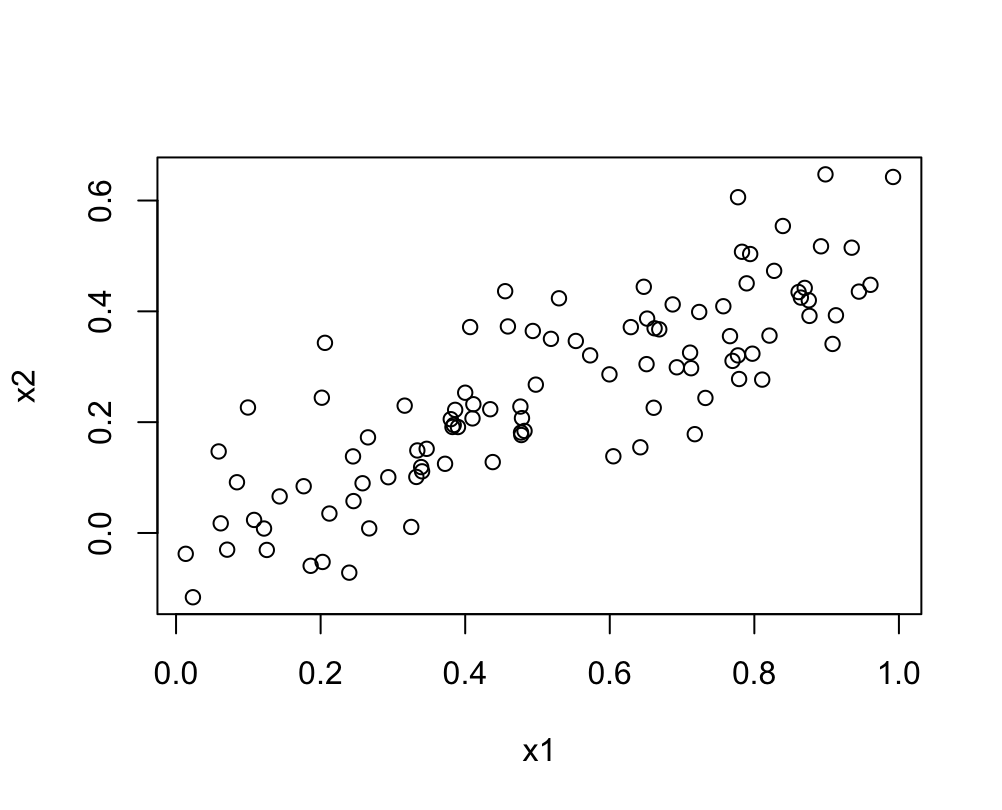 

  

• (c)

  # 14.(c)
  model = lm(y ~ x1+x2)
  summary(model)
  ## β0^=2.1305 β1^=1.4396 β2^=1.0097  β0^与实际值(2)很接近
  ## β1^的p值<0.05，可以拒绝零假设。β1^与实际值(2)有所出入
  ## β2^的p值>0.05，不能拒绝零假设。β2^与实际值大很多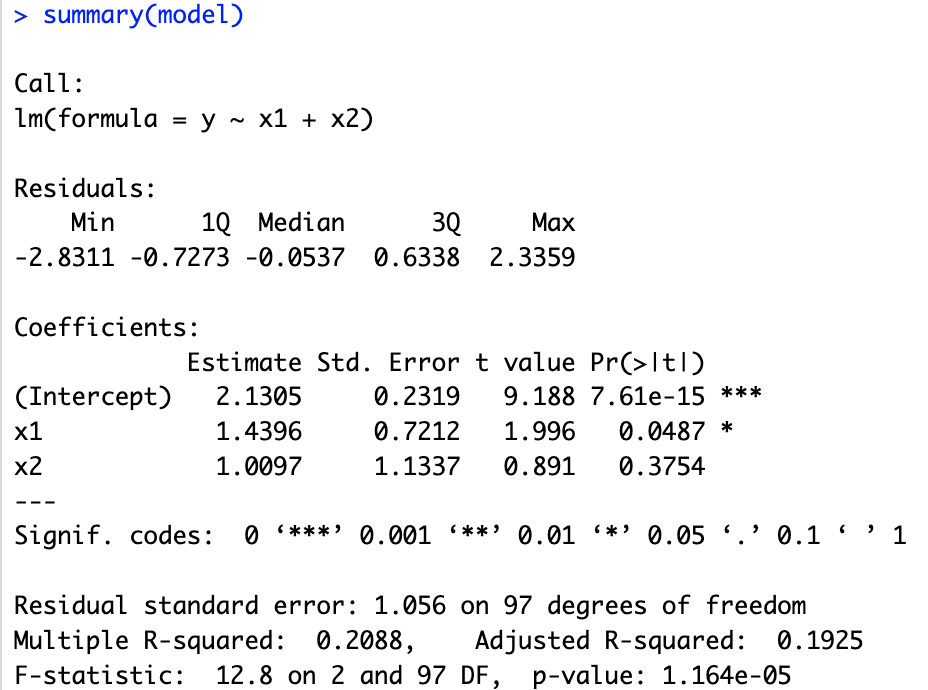

  

• (d)

  # 14.(d)
  model_x1 = lm(y ~ x1)
  summary(model_x1)
  ## 结果的系数很接近真实值，结果的p值远小于0.05，可以拒绝原假设。

  

• (e)

  #  14.(e)
  model_x2 = lm(y ~ x2)
  summary(model_x2)
  ## 结果的系数与真实值差别较大，结果p值小于0.05，可以拒绝原假设。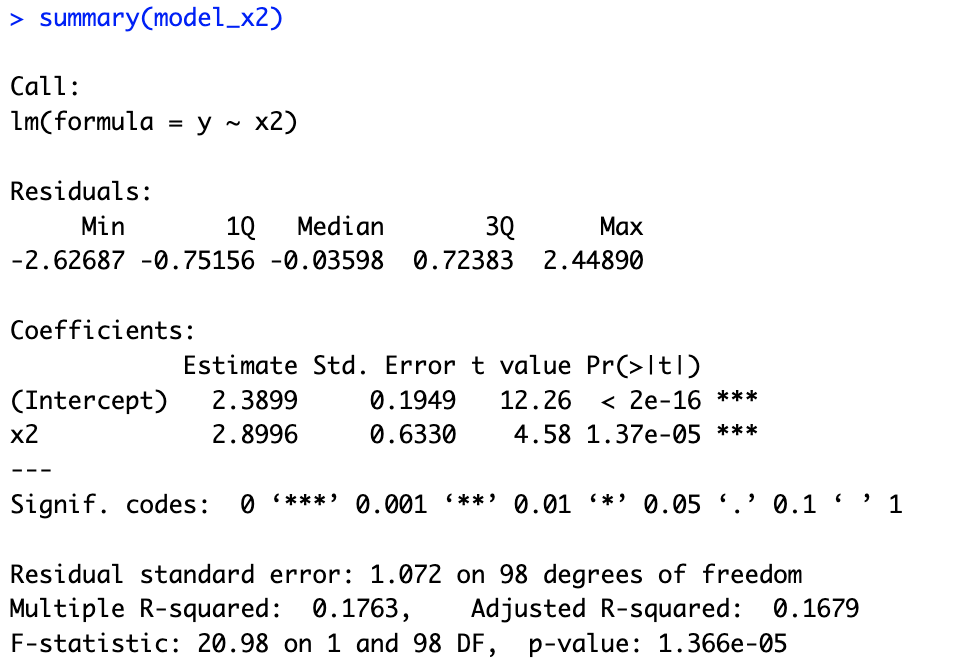

  

• (f)

  # 14.(f)
  ## 不矛盾，因为x2与x1高度线性相关，具有共线性。
  ## 所以在单独拟合时都可以看出与y有显著影响，但是共同拟合的时候无法区分影响。

• (g)

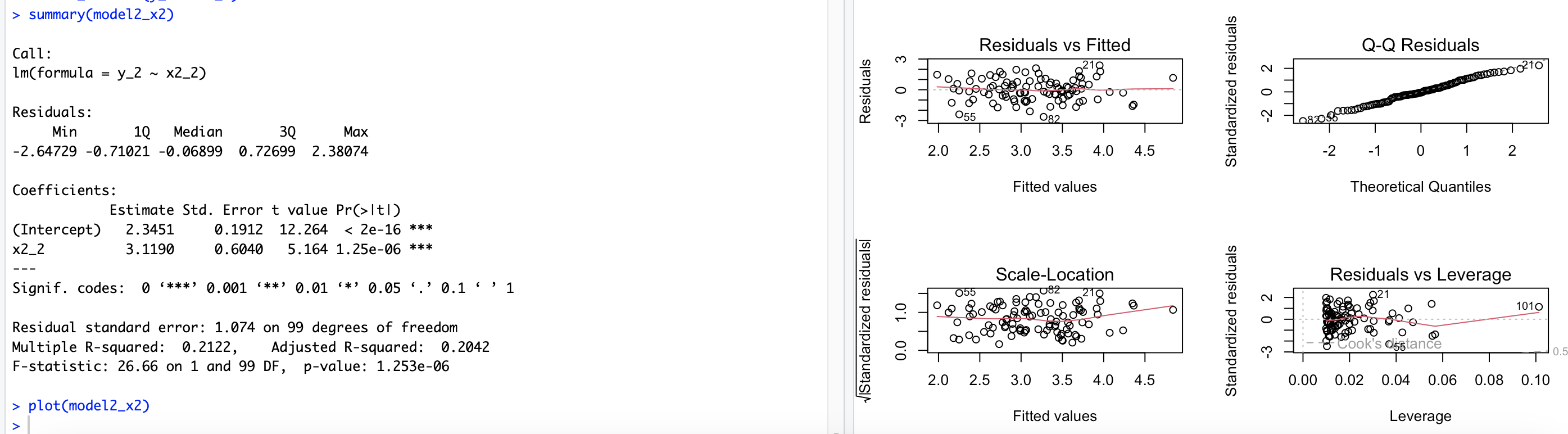
  # 14.(g)
  x1_2 = c(x1, 0.1)  # 在x1变量中添加一个新的数据点0.1
  x2_2 = c(x2, 0.8)  # 在x2变量中添加一个新的数据点0.8
  y_2 = c(y, 6)      # 在y变量中添加一个新的响应变量值6
  par(mfrow=c(2,2))
  model2 = lm(y_2 ~ x1_2 + x2_2)
  summary(model2)
  plot(model2) 
  ## 模型的β0^=2.23 β1^=0.54 β2^=2.51 β1^不能拒绝零假设 β2^可以拒绝零假设（根据p值域0.05关系）
  ## 根据残差-杠杆图可以看出存在明显的高杠杆点（101）
  model2_x1 = lm(y_2 ~ x1_2)
  summary(model2_x1)
  plot(model2_x1)
  ## 模型的β0^=2.25 β1^=1.7 β1^可以拒绝零假设（根据p值域0.05关系）
  ## 根据残差-杠杆图可以看出存在明显的离群点（101、21、55）
  model2_x2 = lm(y_2 ~ x2_2)
  summary(model2_x2)
  plot(model2_x2)
  ## 模型的β0^=2.35 β1^=3.11 β1^可以拒绝零假设（根据p值域0.05关系）
  ## 根据残差-杠杆图可以看出存在明显的离群点（21、55）和高杠杆点（101）

  

  

  

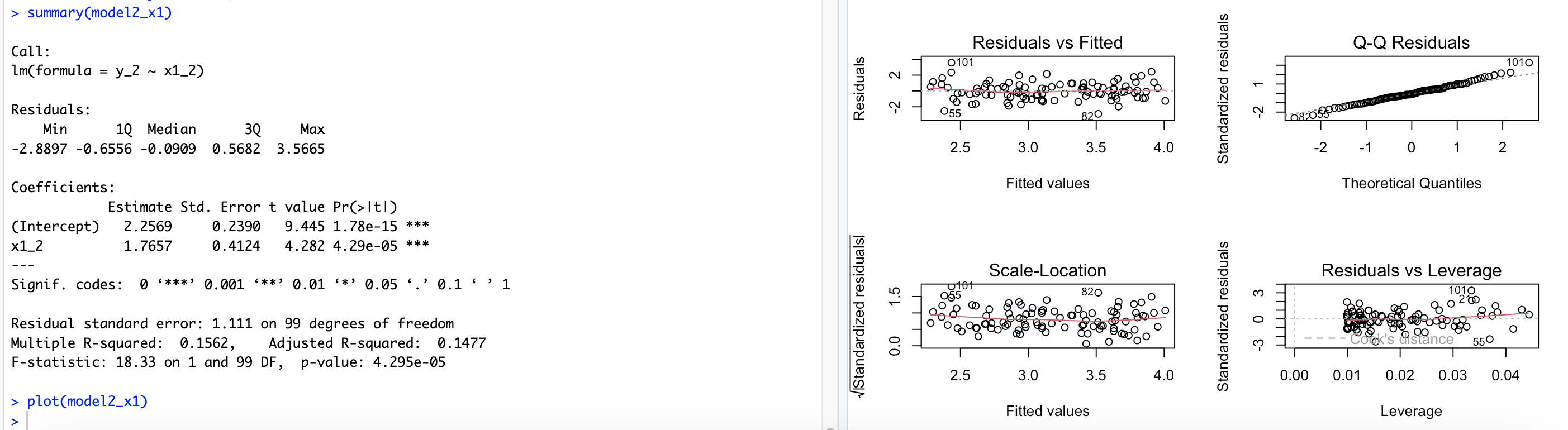
• 完整代码

  # 14.(a)
  set.seed(1)  # 设置随机种子
  x1 = runif(100)  # 生成100个在[0, 1]均匀分布的随机数作为变量x1
  x2 = 0.5 * x1 + rnorm(100) / 10  # 生成变量x2，它与x1高度相关且带有一些随机噪声
  y = 2 + 2 * x1 + 0.3 * x2 + rnorm(100)  # 生成响应变量y，符合给定的线性模型，并添加一些随机噪声
  #回归系数 β0=2 β1=2 β2=0.3
  ​
  # 14.(b)
  par(mfrow=c(1,1))
  cor(x1, x2)  # x1与x2之间的相关系数 0.8351
  plot(x1, x2)  # 绘制x1与x2之间散点图 
  ​
  # 14.(c)
  model = lm(y ~ x1+x2)
  summary(model)
  ## β0^=2.1305 β1^=1.4396 β2^=1.0097  β0^与实际值(2)很接近
  ## β1^的p值<0.05，可以拒绝零假设。β1^与实际值(2)有所出入
  ## β2^的p值>0.05，不能拒绝零假设。β2^与实际值大很多
  ​
  # 14.(d)
  model_x1 = lm(y ~ x1)
  summary(model_x1)
  ## 结果的系数很接近真实值，结果的p值远小于0.05，可以拒绝原假设。
  ​
  #  14.(e)
  model_x2 = lm(y ~ x2)
  summary(model_x2)
  ## 结果的系数与真实值差别较大，结果p值小于0.05，可以拒绝原假设。
  ​
  # 14.(f)
  ## 不矛盾，因为x2与x1高度线性相关，具有共线性。
  ## 所以在单独拟合时都可以看出与y有显著影响，但是共同拟合的时候无法区分影响。
  ​
  # 14.(g)
  x1_2 = c(x1, 0.1)  # 在x1变量中添加一个新的数据点0.1
  x2_2 = c(x2, 0.8)  # 在x2变量中添加一个新的数据点0.8
  y_2 = c(y, 6)      # 在y变量中添加一个新的响应变量值6
  par(mfrow=c(2,2))
  model2 = lm(y_2 ~ x1_2 + x2_2)
  summary(model2)
  plot(model2) 
  ## 模型的β0^=2.23 β1^=0.54 β2^=2.51 β1^不能拒绝零假设 β2^可以拒绝零假设（根据p值域0.05关系）
  ## 根据残差-杠杆图可以看出存在明显的高杠杆点（101）
  model2_x1 = lm(y_2 ~ x1_2)
  summary(model2_x1)
  plot(model2_x1)
  ## 模型的β0^=2.25 β1^=1.7 β1^可以拒绝零假设（根据p值域0.05关系）
  ## 根据残差-杠杆图可以看出存在明显的离群点（101、21、55）
  model2_x2 = lm(y_2 ~ x2_2)
  summary(model2_x2)
  plot(model2_x2)
  ## 模型的β0^=2.35 β1^=3.11 β1^可以拒绝零假设（根据p值域0.05关系）
  ## 根据残差-杠杆图可以看出存在明显的离群点（21、55）和高杠杆点（101）